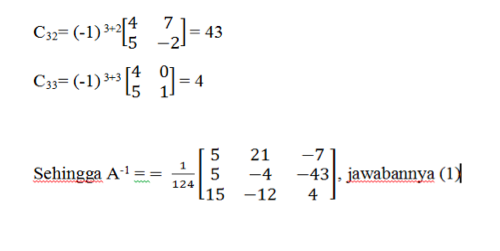invers matriks

 

 Invers Matriks

Invers matriks adalah sebuah kebalikan (invers) dari kedua matriks di mana apabila matriks tersebut dikalikan menghasilkan matriks persegi (AB = BA = |). Simbol dari invers matriks adalah pangkat -1 di atas hurufnya. Contoh matriks B adalah invers matriks A ditulis B = A^–1 dan matriks A adalah invers dari matriks B ditulis A = B^-1. Matriks A dan B merupakan dua matriks yang saling invers (berkebalikan). Invers matriks terdiri dari dua jenis yaitu matriks persegi (_2×2) dan matriks _3×3.
Invers matriks A berordo 2 dapat langsung kita peroleh dengan cara:

1. Tukar elemen-elemen pada diagonal utamanya.
2. Berikan tanda negatif pada elemen-elemen lainnya.
3. Bagilah setiap elemen matriks dengan determinannya.

Rumusan dari invers matriks persegi berordo 2 adalah sebagai berikut:
Jika matriks A = [ a b c d ] dengan determinan A = a.d – b.c, maka invers matriks A dirumuskan sebagai berikut:

Dalam penyelesaian matriks 3 x 3, ada beberapa istilah yang harus kita ketahui yaitu determinan sarrus, minor, kofaktor, dan adjoin. Sebagai contoh apabila terdapat matriks 3 x 3 sebagai berikut: A = [ a b c d e f g h i ]maka rumus untuk mencari inversnya adalah sebagai berikut:

Dari persamaan diatas, ada det (A) yaitu determinan A dan Adj (A) yaitu adjoin A, di mana rumus untuk mencari determinan A menggunakan rumus determinan sarrus yaitu sebagai berikut: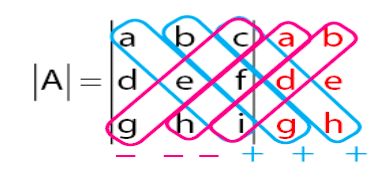

Nilai determinanya sarrusnya menjadi = a x e x | + b x f x g – c x d x h – c x e x g – a x f x h – b x d x |. Selanjutnya penentuan Adjoin A dapat terlihat dari gambar dibawah ini.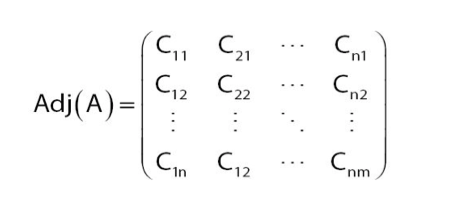

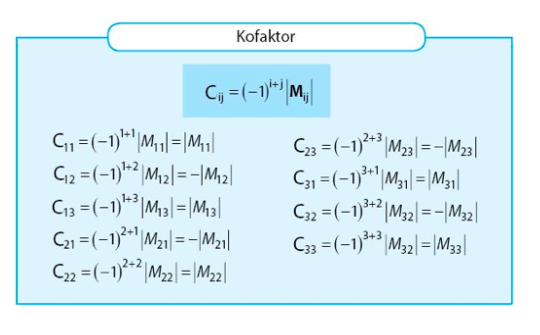
Dari gambar terlihat terdapat simbol C kapital, di mana letak nilai C sudah ditranspos dari baris ke kolom. C merupakan singkatan dari kofaktor. Penentuan nilai kofaktor diperoleh dari penentuan nilai minor suatu matriks. Penentuan nilai kofaktor dan minor adalah sebagai berikut:


Bagaimana Quipperian dengan rumus-rumus di atas? Enggak usah bingung-bingung, cobain dulu nih contoh soal dari Quipper Blog tentang invers matriks 2 x 2 dan invers matriks 3 x 3. Sssttt… Jangan intip jawabannya sebelum kamu jawab sendiri, ya!

Contoh Soal Nomor 1

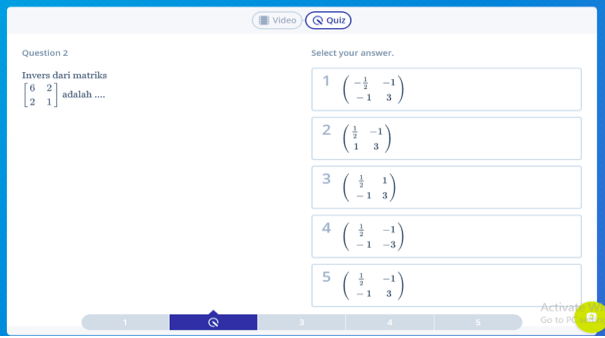
Pembahasan:

Contoh Soal Nomor 2

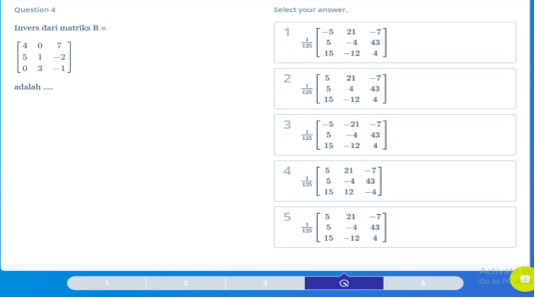
Pembahasan:

Dekomposisi matiks dan determinan matriks

 

Determinan Matriks Metode Crout & DooLittle

Assalamu'alaikum Wr.Wb.

Hai Gaes,

Selamat datang di blog saya, pada bagian ini, saya akan sharing pengetahuan tentang bagaimana cara mengerjakan determinan matriks menggunakan Metode Crout dan Metode DooLittle !

=========================================================

Sedikit Penjelasan:

Tapi disini saya hanya sharing metode crout dan doolittle..

Langsung saja cusss..!

Rumus dari metode crout sendiri yakni sebagai berikut:

untuk kasus matriks berordo 3x3:

matriks yang memiliki a disini adalah matriks yang kita ingin determinankan menggunakan metode crout (setelah sama dengan).

contoh soal ordo 3x3 :

Cara mencari determinannya yaitu dengan mengali diagonal matriks tersebut (dari ujung atas kiri ke ujung kanan bawah), seperti pada contoh matriks diatas, Determinan L = 4 x 10 x 12.

Begitu juga dengan Determinan U = 1 x 1 x 1.

Sehingga, untuk mendapatkan Determinan dari matriks A, kita tinggal mengalikan determinan L dan determinan U.

 Belum Puas dengan Matriks ordo 3x3 ?, baik, saya juga akan share contoh soal dan sedikit pengerjaannya pada Matriks ordo 4x4

=========================================================

Lalu...., Bagaimana dengan Metode DooLittle ??

langsung saja ceikdottt :v

Rumus Metode DooLittle matriks ordo 4x4:

*berikutt ini adalah contoh soal yang beirisikan penjelasan saya sendir i 

*dan bisa diliat penjelasanya melalui link berikut                  https://youtu.be/CKYO27mUicQ